收录于 ACL 2024 best papers

Abstract

之前的研究将“记忆”定义为在训练中使用某个实例对模型预测该实例能力所产生的因果效应。

这一定义依赖于反事实：能观察到如果模型未见过该实例会发生什么情况。

模型可能存储或“记忆”了关于个别训练样本的精确知识。一些先前的研究采用了因果定义来理解记忆：即，在训练过程中观察某个样本对模型正确预测该样本能力所产生的因果效应。观念直观，但不容易量化需要反事实案例——我们需要知道没有被训练过这个样本，LLM会表现为什么样子。

作者首先将反事实记忆形式化为两种潜在结果之间的差异，作者推广了以往对记忆的定义，是我们能够在统一框架下比较不同的定义。使用观测数据来估计记忆，只需要模型在整个训练过程中对一小部分训练数据的表现指标。方法的输出被称为“记忆特征”：即模型在训练过程中对各个训练批次的记忆程度。

本文提出了一种基于计量经济学中“差分法”设计的新方法，以原理清晰高效的的方式估计记忆趋势，仅需要观察模型在训练过程中对少量实例的表现，

更大的模型表现出更强且更持久的记忆；
记忆程度受数据顺序和学习率的影响；
不同规模模型之间的记忆趋势具有一致性，因此可以通过小模型预测大模型的记忆行为。

Dataset：Pile

Baseline：

LLM：Pythia

Background

语言建模

设$p _\theta(x)$是一个参数为$\theta \in \mathbb{R}^d$的语言模型，该模型定义了所有可以从字母表V中的元素构造出的有限序列集合$x \in V^*$上的概率分布，从一组随机选择的初始参数$\theta _0$开始，使用一个数据集D和一个基于损失函数L定义的优化过程来学习参数θ。设$D = { x_n } _{n=1}^{N}$是一个数据集，其中每个样本x是从目标分布p(x)中采样的序列。假设这些样本是独立同分布，并通过一个排列函数$\sigma: {1, \ldots, N} \to {1, \ldots, N}$进行打乱，给定一个批大小B，将这个数据集划分为$T \leq \left\lfloor \frac{N}{B} \right\rfloor$个批次$B _t$，然后依次对这些批次进行迭代，并对模型参数执行梯度更新：

$$ \theta_t = \theta_{t-1} - \eta \nabla_{\theta} L(\theta_{t-1}, B_t) $$

其中$\eta∈R$是学习率。这种训练方式是对训练集的一次完整遍历，也是近期语言模型的标准做法。

在每次迭代时，使用一个批次$B _t$得到一个新的模型检查点$\theta _t$，引入一种记号来区分检查点与批次的索引。用$c∈{0,1, \ldots ,T}$表示检查点步数（如$\theta _c$）。此外，用$g \in {1, \ldots, T} \cup {\infty}$表示某个批次用于训练的时间步（例如$B _g$），将其称为“处理时间步”。将$g=∞$表示由为用于训练、仅用于验证的实例组成的批次，即验证集。

因果分析

因果分析通常分为三个步骤：

定义一个因果估计目标（causal estimand），也就是我们希望估计的目标量；
将这个因果估计目标转化为可观测数据所需的假设，从而定义一个统计估计目标（statistical estimand），这个过程被称为识别；
定义一个估计器（estimator），即用来近似统计估计目标的统计方法。

为了将记忆定义为一个因果估计目标，作者使用Rubin提出的潜在结果框架。对x的训练定义了“处理”，而模型对该实例的预测能力定义了“结果”。

由于训练是按批次逐步进行的，因此不同的实例会在不同的时间步受到处理。作者使用了一个处理分配变量G(x)来表示某个实例是在哪一步g被训练的。为了量化参数为$\theta_c$的模型对x的预测能力，使用一个性能函数 $γ$。定义结果变量为：
$$
Y_c(x) \triangleq \gamma(\theta_c, x)
$$
将此性能函数设为x在$p_{\theta c}$下的对数似然：
$$
\gamma(\theta_c, x) = \log p_{\theta_c}(x)
$$
要定义“记忆”，需要同时考虑观察到的结果（即 $Y_c(x)$ ）和反事实结果（即如果我们没有训练该实例时模型在该实例上的表现）。潜在结果记号（Splawa-Neyman, 1923）使我们能够一致地表示这两种类型的结果。

定义1：

在时间步c、处理分配为g的情况下，实例x的潜在结果记作$Y_c(x;g)$，表示如果$G(x)=g$，那么结果变量所应具有的值。

由于只观察到了一次数据的排列，因此对于每个实例x，我们只能看到一个特定的处理时间步G(x)。因此，只有当处理分配g=G(x)时，我们才能观察到该实例的潜在结果。在这种情况下，我们可以将潜在结果等同于观察结果，即

$ Y_c(x;g)=Y_c(x) $，该性质称为一致性。而对于任何其他处理时间步g≠G(x)，潜在结果都是反事实的，incident无法从数据中直接观测到。

Method

反事实记忆

反事实记忆可以理解为对以下问题的回答：

"如果我们在时间步 g 没有训练实例 x ，那么在时间步 c 模型对该实例的表现会有什么不同？ "

定义2：

反事实记忆是指在观测到的时间步G(x)=g对实例x进行训练，对模型在时间步c上对该统一实例表现所产生的因果效应：

$$ \tau_{x,c} \overset{\text{def}}{=} \underbrace{Y_c(x; g)}_{\text{训练时包含 x 时在 x 上的表现}} - \underbrace{Y_c(x; \infty)}_{\text{未见过 x 时在 x 上的表现}} $$

公式2被称为个体处理效应（Individual Treatment Effect, ITE），该式中的第一个潜在结果$ Y_c(x;g)$时可以从数据中观察到的，因为我们在时间步G(x)=g训练了该实例。然而，第二项 $Y_c(x;∞)$ 是反事实的 。要计算这个ITE，我们需要估计特定实例的反事实结果，但由于未观测因素和异质性，这在实践中具有挑战性。

尽管理想情况下希望在单个实例层面估计记忆程度，但出于计量经济学文献常见做法，我们关注平均效应。

定义3：

预期反事实记忆是指在时间步 g 使用某些实例进行训练，对模型在时间步 c 上对这些相同实例表现所产生的平均因果效应：

$$ \tau_{g,c} \overset{\text{def}}{=} \mathbb{E}_x \left[ Y_c(x; g) - Y_c(x; \infty) \mid G(x) = g \right] $$

异质性指的是不同样本对训练的反应可能不用。所有$\tau_{g,c}$组成一个举证，称为模型的记忆特征，其中每一行代表一个批次的记忆路径。记忆特征与记忆路径是我们能够分析模型在不同处理时间步与检查点时间步下的记忆模式。

当c<g时，不可能存在记忆，因此此时模型尚未见过这些实例，因此在这种情况下$\tau_{g,c}=0$.

当 c=g 时的 $\tau_{g,c}$称为即时记忆 （instantaneous memorisation），模型刚训练完该样本就表现出记忆;
当 c>g 时的$\tau_{g,c}$ 称为持续记忆 （persistent memorisation），在后续时间步仍保持对该样本的记忆;
当 c=T 时的 $\tau_{g,c}$ 称为残余记忆 （residual memorisation），最终模型仍然记得该样本。

记忆的估计

将记忆定义在处理时间步 g 层面的实际含义是：我们只能对在同一时间步被训练的样本组 （即批次 $B_g$ ）做出因果推断，而不能针对单个实例进行。

$$ \begin{equation} \tau_{g,c} = \underbrace{\mathbb{E}_x \left[ Y_c(x; g) \mid G(x)=g \right]}_{1} - \underbrace{\mathbb{E}_x \left[ Y_c(x; \infty) \mid G(x)=g \right]}_{2} \end{equation} $$

项 1 可以直接从数据中估计，因为批次 $B_g$ 中的样本都满足 G(x)=g ，我们可以利用一致性假设，将 $Y_c(x;g)$ 等同于观察到的结果 $Y_c(x)$。

定义一个批次中所有样本的平均表现为：

$$ \begin{equation} Y_c(g) \overset{\text{def}}{=} \frac{1}{|B_g|} \sum_{x \in B_g} Y_c(x) \end{equation} $$

项 2 是反事实的：我们无法观察那些“从未被训练”的情况下模型的表现$Y_c(x;∞)$ 。

因果估计目标中包含反事实潜在结果，这使得估计变得困难，这也是因果推理中的基本难题 。因此，因果方法的目标就是通过可观测的数据去估计这些反事实结果，通常依赖于可比的样本组。

差分估计器（Difference Estimator）

第一个估计记忆的方法，只需要验证集上观察结果，但依赖于一个较强的识别假设。

假设1：

实例x是独立同分布地从p(x)中采样的，并被随机分配到不同的处理组g。在此假设下，有：

$$ \begin{equation} \tau^{\text{diff}}_{g,c} = \mathbb{E}_x \left[ Y_c(x; g) \mid G(x)=g \right] - \mathbb{E}_x \left[ Y_c(x; \infty) \mid G(x)=\infty \right] \end{equation} $$

与公式 (3) 不同的是，这里的第二项不是反事实——它是验证集实例$B_∞$ 的期望观测结果。

使用如下估计器：

估计器1（差分估计器）：

$$ \begin{equation} \tau^{\text{diff}}_{g,c} = Y_c(g) - Y_c(\infty) \end{equation} $$

在假设成立的情况下，这是一个无偏估计器。

即使假设 1 成立，上述公式要想具有低方差，也需要足够大的样本量来计算 $Y_c(g)$ 和 $Y_c(∞)$ 。然而，考虑到当前最先进的语言模型及其训练集的规模，为所有实例 x 和检查点 c 提取性能指标$Y_c(x)$在计算和内存上都非常昂贵。

差分中的差分估计器

作者现在引入了一种基于“差分中的差分”（Difference-in-Differences, DiD）设计因果估计器，DiD的核心思想是利用时间维度来辅助设别，通过比较受训样本与未受训样本在时间趋势上的差异，来识别因果效应。

DiD 基于以下假设：如果没有被用于训练，不同批次在模型表现上的变化趋势应该是相似的。

假设 2（平行趋势） ：

在没有训练的情况下，模型在不同检查点之间的表现变化趋势对于不同处理组是相同的。即对于任意c,c’≥g-1：

$$ \begin{equation} \mathbb{E}_x \left[ Y_c(x; \infty) - Y_{c'}(x; \infty) \mid G(x)=g \right] = \mathbb{E}_x \left[ Y_c(x; \infty) - Y_{c'}(x; \infty) \mid G(x)=\infty \right] \end{equation} $$

在应用DiD设计之前，还需要第二个假设：

假设3（无预期效应）：

训练在发生之前不会产生影响，即对任意c<g：

$$ \begin{equation} \mathbb{E}_x \left[ Y_c(x; g) \mid G(x)=g \right] = \mathbb{E}_x \left[ Y_c(x; \infty) \mid G(x)=g \right] \end{equation} $$

（c是检查时间步，g是训练时间步，在未被训练之前，在样本被训练之前，模型对他们的表现应该和从未被训练过一样。）

有：

$Y_c(x;∞),Y_{g−1}(x;∞)$ 在验证集上可观测；
$Y_{g−1}(x;g)$在训练集上可观测。

由此可以得到以下统计估计目标：

$$ \begin{equation} \tau^{\text{did}}_{g,c} = \mathbb{E}_x \left[ Y_c(x; g) - Y_{g-1}(x; g) \mid G(x)=g \right] - \mathbb{E}_x \left[ Y_c(x; \infty) - Y_{g-1}(x; \infty) \mid G(x)=\infty \right] \end{equation} $$

由此得到以下DiD估计器：

估计器2（DiD估计器）：

$$ \begin{equation} \tau^{\text{did}}_{g,c} = \left( Y_c(g) - Y_{g-1}(g) \right) - \left( Y_c(\infty) - Y_{g-1}(\infty) \right) \end{equation} $$

DiD估计器所依赖的假设更弱，且在温和条件下具有比公式7中差分估计器更低的方差。

能这么做的原因是作者假设在不同的样本上面，我们的趋势是一致的，所以在训练集和验证集上面去观察在g时的趋势。

差分估计器是比较训练组和验证组在同一时间点的表现；

DiD估计器是比较两组在两个时间点之间的趋势差异。

记忆的定义

反事实记忆的已有操作化定义

令ψ 是一个变量向量，用于表示训练过程中的随机性来源，例如由排列函数 σ 引起的数据顺序变化、以及初始参数 $θ_0$ 。通过定义这些变量上的分布 p(ψ) ，我们可以如下定义架构层面的记忆。

定义4：

当对训练变量ψ进行边缘化时，反事实记忆$τ_{x,T}$，被定义为：

$$ \begin{equation} \tau_{x,p(\psi)} \overset{\text{def}}{=} \mathbb{E}_\psi \left[ \tau_{x,T} \mid G(x)=\infty \right] = \mathbb{E}_\psi \left[ Y_T(x; G(x)) - Y_T(x; \infty) \mid G(x)=\infty \right] \end{equation} $$

其中第一个潜在结果中的G(x)取决于打乱函数σ将x分配到哪个批次。

最简单估计这个值的方法：在包含或不包含x的数据集上分别训练多个模型，并用这些模型去近似上述期望——但是计算成本高，且：

它无法提供关于检查点步数或处理步数对记忆影响的洞察；这是因为 T 被硬编码进 $τ_{x,p(ψ)}$ 的定义中，并且它对数据排列进行了边缘化。虽然可以将该定义推广到其他检查点步数 c 或特定的 g ，但以往研究主要关注这些特定选择，忽略了训练动态对记忆的影响。
也许更重要的是，对 p(ψ) 进行边缘化意味着该指标衡量的是模型架构 的记忆能力，而不是具体模型实例 的记忆能力。

影响函数

影响函数用于在不重新训练模型的前提下，估计如果从训练集中移除某个样本x，模型参数会如何变化。

新的参数集合可以通过以下方式近似：

$$ \begin{equation} \theta_{-x,T} \approx \theta_T + \frac{1}{N} H^{-1}_\theta \nabla_\theta L(\theta_T, x) \end{equation} $$

其中$H_\theta$是损失函数L在$\theta_T$处的海森矩阵。

该近似居于围绕$\theta_T$的一阶泰勒展开，并在以下假设下误差较小：

损失函数在 θ 上严格凸；
海森矩阵$H_\theta$是正定矩阵；
模型已经收敛（即梯度为零）。

在这些假设下，影响函数可用于高效的估计反事实项$Y_T(x;∞) $，即如果没有训练过x时的表现。

可以使用更新后的参数来测量模型表现：

$$ \begin{equation} \hat{\tau}^{\text{infl}}_{x,T} = Y_T(x) - Y_{-x,T}(x) \end{equation} $$

并设定$ Y _T(x;∞)=Y _{−x,T(x)}$，记忆的影响函数估计器可写为：

$$ \begin{equation} \hat{\tau}^{\text{infl}}_{x,T} = Y_T(x) - Y_{-x,T}(x) \end{equation} $$

影响函数提供了一种计算效率较高的方法来估计实例级别的反事实记忆。然而，语言模型通常并不满足上述任一假设，这可能导致该估计器出现严重偏差。

可提取记忆

将记忆定义为(k,l)-可提取性(extractability)：如果给定一个长度为k的前缀，模型能正确预测接下来的l的token，则在字符串是*(k,l)-可提取性*。

作者假设可提取记忆本质上是一种反事实记忆的估计器。

设性能函数 γ衡量一个字符串是否是*(k,l)-可提取性*，再假设在未训练的情况下，一个字符串不是*(k,l)-可提取性*的，即$Y_c(x;∞) =0$。在这一假设下，可以定义一个可提取记忆估计器为：

$$ \begin{equation} \tau^{\text{extr}}_{x,c} = Y_c(x) \end{equation} $$

可提取记忆隐含地假设$Y _c(x;∞) =0$，而反事实记忆则明确控制这一反事实项，值得注意的是，在字符串较长且复杂的情况下，这一假设可能是合理的，因为这种情况下，该字符串出现在模型top-1 beam（贪婪解码输出）中的概率趋近于零。但对于较短或结构简单的序列，这一假设可能并不成立，相反可能导致结果混淆了记忆和预测难度两个因素。

Experiment

Pythia套件

作者使用公开可用的Pythia模型套件，其中包含8个不同大小的Transformer模型，规模参数在70M到12B不等。在Pile数据集上训练，这是一个包含3000亿token的英文文档集合。所有模型使用相同的数据进行训练，数据集被打乱并打包成长度为2049的序列，每个这样的序列对应一个实例x。训练过程中使用了带有warm-up的余弦学习率调度器，并采用1024个序列的批量大小，最终进行了143000次优化步骤。

使用去重后的 Pile 数据集版本来减少因重复导致的虚假记忆模式。去重后的数据集包含 2070 亿 token，因此使用这个版本的模型需要训练大约 1.5 个 epoch，以保持与未去重版本相同的 token 数量。我们考虑的是第一个 epoch 内的检查点（即最多到第 95,000 步）。

创建面板数据

考虑Pile数据集的规模，在所有实例上进行评估在计算上不可行，因此只对数据进行子采样。

现有检查点的时间粒度（1000步）不允许考虑每一个时间步，因此我们只考虑步数$c∈ { 0,1k,…,95k}$和处理时间步$g∈ { 0,1k,…,95k}$。为了匹配检查点频率，我们将两个检查点之间的所有批次认为在同一时间步被模型观察到，称之宏批次。

为了获得每个宏批次的足够评估次数，作者分两步从训练集中采样实例：首先随机选择每个宏批次的10个批次，然后从每个批次中再采样10个实例。这一过程最终得到14300个训练实例。作者还在验证集中采样2000个实例用于构建未参与训练的宏批次。最终得到了一个包含16,300 个实例、在 96 个时间步上评估的面板数据。

性能指标使用的是序列级别的对数似然：

$$ \gamma(\theta, x) = \log p_\theta(x) $$

统计推断

为了计算统计显著性，采用简单乘数引导程序，该程序返回所有记忆估计值的同时置信区间，考虑到宏批次和检查点步数之间的依赖关系，从而避免多重检验问题。

Results

即时记忆

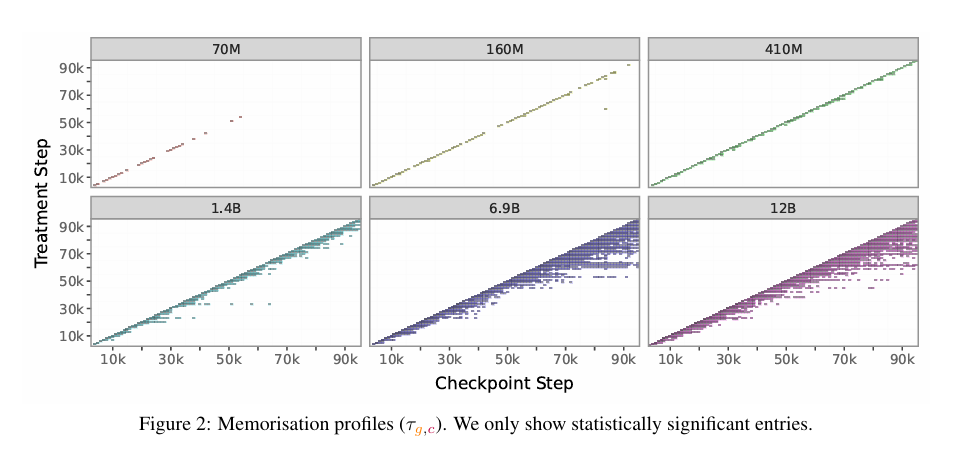
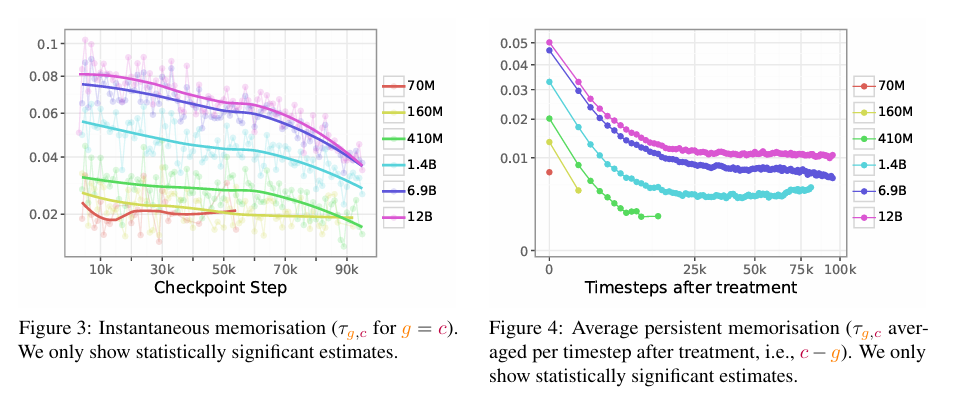
即时记忆估计值（在第 3 节中定义为$\tau_{g,c}$当 g=c 时）显示在图 2 的记忆特征对角线上，并也在图 3 中展示。从这些估计值中，我们可以清楚地观察到处理步数对记忆的影响：训练早期的即时记忆比后期更强。有趣的是（但也许并不令人惊讶），即时记忆与余弦学习率调度密切相关：它在 warm-up 阶段后（大约第 1,500 步）比之前更强。此外，正如预期，即时记忆随着模型规模的增加而增强。

值得注意的是，我们预计在正常训练的语言模型中总会存在一定程度的即时记忆（尽管可能值很小）。因此它可以用于功效分析（Cohen, 1992）：选择每个宏批次应采样的实例数量，以提供足够的统计功效来正确检测记忆现象。

持续记忆

持续记忆估计值（在第 3 节中定义为$$\tau_{g,c}$$当 g>c 时）显示在图 2 的记忆特征非对角线上。图 4 显示了特定处理后时间步数下的平均持续记忆；在这个图中，$$\tau_{g,c}$$ 在每个 c−g 上跨宏批次取平均。这种聚合方式使我们能够总结模型的一般记忆模式。较小的模型具有较低的持续记忆，其中 70M 模型几乎没有持续记忆。有趣的是，持续记忆在 25,000 步后趋于稳定。这一结果对训练期间的数据顺序安排有影响。例如，如果我们有一些不希望模型记住但仍想在训练中使用的实例，它们应该被安排在较早的批次中。

通过跨宏批次取平均，方差更低，更多的估计值变得具有统计显著性。

残余记忆

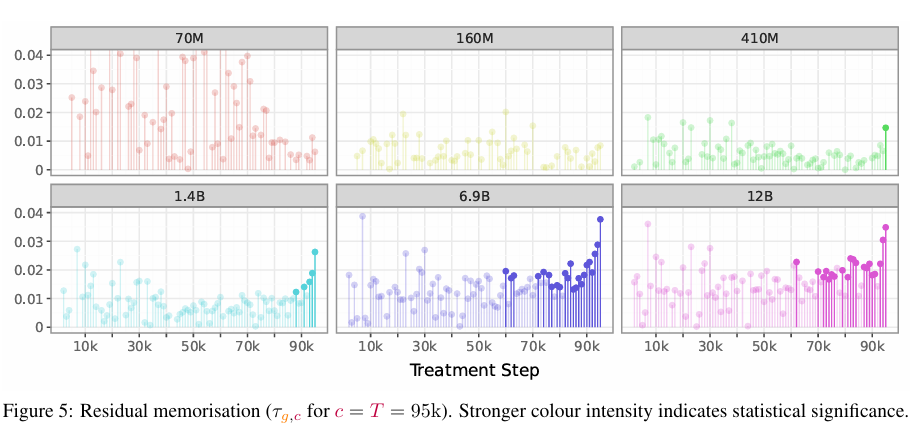
残余记忆估计值（在第 3 节中定义为 $\tau_{g,c}$当 c=T 时）显示在图 2 的最后一列中，并在图 5 中也展示（在这里我们考虑 T 为第一个 epoch 的结束，即第 95,000 步）。有趣的是，虽然所有宏批次都经历了某种程度的即时记忆，但如图所示，许多宏批次在第一个 epoch 结束时已被遗忘，因为残余记忆估计值在统计上不显著。此外，与我们的持续记忆结果一致，残余记忆也表现出近期效应：最后几个宏批次的记忆最强。我们假设这种近期效应可以用学习率调度来解释。具体来说，当学习率较高时，优化过程会使模型参数朝着局部最优方向移动更远，从而用新信息覆盖旧信息；这导致更高的即时记忆和更低的残余记忆。相反，在训练过程接近尾声、学习率较低时，由于更新幅度变小（期望值意义上），旧信息被“遗忘”的程度较低，从而导致更高的残余记忆和更低的即时记忆。

我们注意到我们的结果与 Biderman 等人（2023b）有所不同，他们发现实例的处理步数对记忆没有差异。我们推测这种差异源于用于量化记忆的指标和采用的统计方法的不同。

不同规模下的记忆

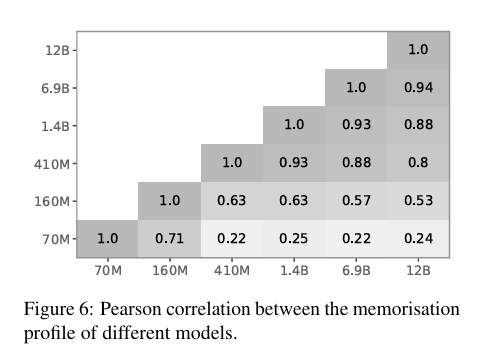
由于训练大型语言模型的成本高昂，在实际训练之前预测模型特性是非常有价值的。一种策略是从较小的模型中获取洞察，以指导更大模型的设计。不同规模下的可预测性在图 3 和图 4 中非常直观，因为不同模型规模之间呈现出相似的趋势。我们在图 6 中正式表达了这一直觉，其中我们报告了不同模型记忆特征之间的皮尔逊相关系数。有趣的是，较大模型（如 12B）的记忆可以从较小模型（如 410M）中预测。我们注意到 70M 和 160M 模型对 12B 模型的记忆预测能力较差。然而，先前的研究表明这两个模型都存在训练不稳定的问题（Godey 等人，2024）；因此，这种预测能力的下降可能是 Pythia 套件特有的。

]